ARITHMETIC PROGRESSION

Arithmetic Sequences

An Arithmetic Sequence is made by adding the same value each time.

Example:

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

This sequence has a difference of 3 between each number.
The pattern is continued by adding 3 to the last number each time, like this:

Example:

3, 8, 13, 18, 23, 28, 33, 38, ...

This sequence has a difference of 5 between each number.
The pattern is continued by adding 5 to the last number each time, like this:

The value added each time is called the "common difference"

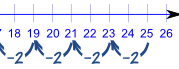
What is the common difference in this example?

19, 27, 35, 43, ...

Answer: The common difference is 8

The common difference could also be negative:

Example:

25, 23, 21, 19, 17, 15, ...

This common difference is −2
The pattern is continued by subtracting 2 each time, like this:

Special Sequences

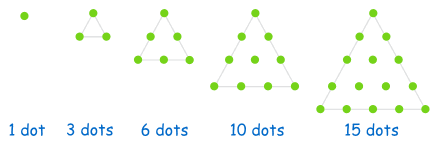
Triangular Numbers

1, 3, 6, 10, 15, 21, 28, 36, 45, ...

This Triangular Number Sequence is generated from a pattern of dots which form a triangle.

By adding another row of dots and counting all the dots we can find the next number of the sequence:

Square Numbers

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, ...

They are the squares of whole numbers:

0 (=0×0)
1 (=1×1)
4 (=2×2)
9 (=3×3)
16 (=4×4)
etc...

Cube Numbers

1, 8, 27, 64, 125, 216, 343, 512, 729, ...

They are the cubes of the counting numbers (they start at 1):

1 (=1×1×1)
8 (=2×2×2)
27 (=3×3×3)
64 (=4×4×4)
etc...

Fibonacci Numbers

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

The Fibonacci Sequence is found by adding the two numbers before it together.
The 2 is found by adding the two numbers before it (1+1)
The 21 is found by adding the two numbers before it (8+13)
The next number in the sequence above would be 55 (21+34)

Can you figure out the next few numbers?

( https://www.mathsisfun.com/algebra/sequences-sums-arithmetic.html )