Geometric Sequences
In a Geometric Sequence each term is found by multiplying the previous term by a constant.
In General we write a Geometric Sequence like this:
{a, ar, ar2, ar3, ... }
where:
- a is the first term, and
- r is the factor between the terms (called the "common ratio")
But be careful, r should not be 0:
- When r=0, we get the sequence {a,0,0,...} which is not geometric
The Rule
We can also calculate any term using the Rule:
xn = ar(n-1)
(We use "n-1" because ar0 is for the 1st term)
A Geometric Sequence can also have smaller and smaller values:
Why "Geometric" Sequence?
Because it is like increasing the dimensions in geometry:
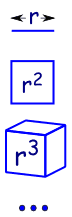 | a line is 1-dimensional and has a length of r |
| in 2 dimensions a square has an area of r2 | |
| in 3 dimensions a cube has volume r3 | |
| etc (yes we can have 4 and more dimensions in mathematics). |
Geometric Sequences are sometimes called Geometric Progressions (G.P.’s)
Summing a Geometric Series
When we need to sum a Geometric Sequence, there is a handy formula.
To sum:
a + ar + ar2 + ... + ar(n-1)
Each term is ark, where k starts at 0 and goes up to n-1
Use this formula:
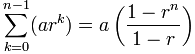
a is the first term
r is the "common ratio" between terms
n is the number of terms
What is that funny symbol? It is called Sigma Notation
| (called Sigma) means "sum up" |
And below and above it are shown the starting and ending values:
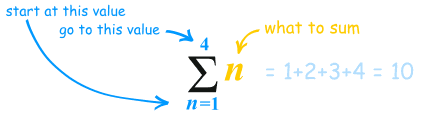
It says "Sum up n where n goes from 1 to 4. Answer=10
The formula is easy to use ... just "plug in" the values of a, r and n
Using the Formula
Let's see the formula in action:
And another example, this time with r less than 1:
Why Does the Formula Work?
Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.
| First, call the whole sum "S": | S = | a + ar + ar2 + ... + ar(n-2)+ ar(n-1) | |
| Next, multiply S by r: | S·r = | ar + ar2 + ar3 + ... + ar(n-1) + arn |
Notice that S and S·r are similar?
Now subtract them!
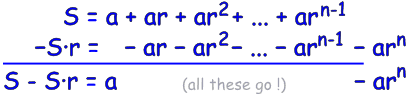
Wow! All the terms in the middle neatly cancel out.
(That is a neat trick!)
(That is a neat trick!)
By subtracting S·r from S we get a simple result:
S − S·r = a − arn
Let's rearrange it to find S:
| Factor out S and a: | S(1−r) = a(1−rn) | |
| Divide by (1-r): | S = a(1−rn)/(1−r) |
Which is our formula (ta-da!):
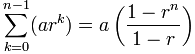
Infinite Geometric Series
So what happens when n goes to infinity?
Well ... when r is less than 1, then rn goes to zero and we get:
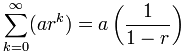
NOTE: this does not work when r is 1 or more (or less than -1):
r must be between (but not including) -1 and 1
and r should not be 0 because we get the sequence {a,0,0,...} which isn't geometric
Let's bring back our previous example, and see what happens:
Don't believe me? Just look at this square:
By adding up (1/2)+(1/4)+(1/8)+...
... we end up with the whole thing!
|  |
Recurring Decimal
On another page we asked "Does 0.999... equal 1?", well, let us see if we can calculate it:
So there we have it ... Geometric Sequences (and their sums) can do all sorts of amazing and powerful things.
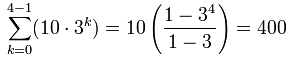
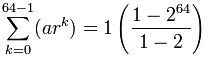
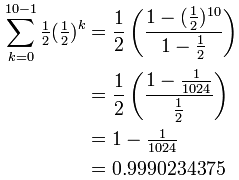
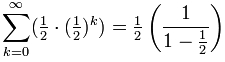
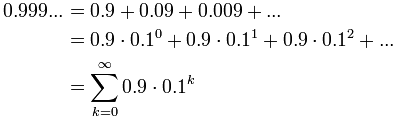
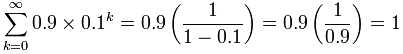
Tiada ulasan:
Catat Ulasan