LOGARITHMS

Introduction to Logarithms

In its simplest form, a logarithm answers the question:

How many of one number do we multiply to get another number?

Example: How many 2s do we multiply to get 8?

Answer: 2 × 2 × 2 = 8, so we needed to multiply 3 of the 2s to get 8

So the logarithm is 3

How to Write it

We write "the number of 2s we need to multiply to get 8 is 3" as:

log₂(8) = 3

So these two things are the same:

The number we are multiplying is called the "base", so we can say:

• "the logarithm of 8 with base 2 is 3"
• or "log base 2 of 8 is 3"
• or "the base-2 log of 8 is 3"

Notice we are dealing with three numbers:

• the base: the number we are multiplying (a "2" in the example above)
• how many times to use it in a multiplication (3 times, which is the logarithm)
• The number we want to get (an "8")

More Examples

Example: What is log₅(625) ... ?

We are asking "how many 5s need to be multiplied together to get 625?"

5 × 5 × 5 × 5 = 625, so we need 4 of the 5s

Answer: log₅(625) = 4

Example: What is log₂(64) ... ?

We are asking "how many 2s need to be multiplied together to get 64?"

2 × 2 × 2 × 2 × 2 × 2 = 64, so we need 6 of the 2s

Answer: log₂(64) = 6

Exponents

Exponents and Logarithms are related, let's find out how ...

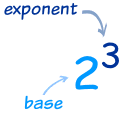The exponent says how many times to use the number in a multiplication. In this example: 23 = 2 × 2 × 2 = 8 (2 is used 3 times in a multiplication to get 8)

So a logarithm answers a question like this:

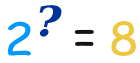
In this way:

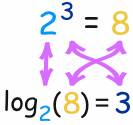
The logarithm tells us what the exponent is!

In that example the "base" is 2 and the "exponent" is 3:

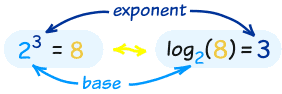
So the logarithm answers the question:

What exponent do we need 
(for one number to become another number) ?

The general case is:

Example: What is log₁₀(100) ... ?

10² = 100

So an exponent of 2 is needed to make 10 into 100, and:

log₁₀(100) = 2

Example: What is log₃(81) ... ?

3⁴ = 81

So an exponent of 4 is needed to make 3 into 81, and:

log₃(81) = 4

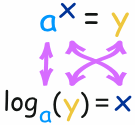
Common Logarithms: Base 10

Sometimes a logarithm is written without a base, like this:

log(100)

This usually means that the base is really 10.

It is called a "common logarithm". Engineers love to use it.

On a calculator it is the "log" button.

It is how many times we need to use 10 in a multiplication, to get our desired number.

Example: log(1000) = log₁₀(1000) = 3

Natural Logarithms: Base "e"

Another base that is often used is e (Euler's Number) which is about 2.71828.

This is called a "natural logarithm". Mathematicians use this one a lot.

On a calculator it is the "ln" button.

It is how many times we need to use "e" in a multiplication, to get our desired number.

Example: ln(7.389) = log_e(7.389) ≈ 2

Because 2.71828² ≈ 7.389

But Sometimes There Is Confusion ... !

Mathematicians use "log" (instead of "ln") to mean the natural logarithm. This can lead to confusion:

Example	Engineer Thinks	Mathematician Thinks
log(50)	log10(50)	loge(50)	confusion
ln(50)	loge(50)	loge(50)	no confusion
log10(50)	log10(50)	log10(50)	no confusion

So, be careful when you read "log" that you know what base they mean!

Logarithms Can Have Decimals

All of our examples have used whole number logarithms (like 2 or 3), but logarithms can have decimal values like 2.5, or 6.081, etc.

Example: what is log₁₀(26) ... ?

Get your calculator, type in 26 and press log Answer is: 1.41497...

The logarithm is saying that 10^1.41497... = 26
(10 with an exponent of 1.41497... equals 26)

This is what it looks like on a graph: See how nice and smooth the line is.

Read Logarithms Can Have Decimals to find out more.

Negative Logarithms

−	Negative? But logarithms deal with multiplying. What could be the opposite of multiplying? Dividing!

A negative logarithm means how many times to divide by the number.

We could have just one divide:

Example: What is log₈(0.125) ... ?

Well, 1 ÷ 8 = 0.125,

So log₈(0.125) = −1

Or many divides:

Example: What is log₅(0.008) ... ?

1 ÷ 5 ÷ 5 ÷ 5 = 5⁻³,

So log₅(0.008) = −3

It All Makes Sense

Multiplying and Dividing are all part of the same simple pattern.

Let us look at some Base-10 logarithms as an example:

	Number	How Many 10s	Base-10 Logarithm
	.. etc..
	1000	1 × 10 × 10 × 10	log10(1000)	= 3
	100	1 × 10 × 10	log10(100)	= 2
	10	1 × 10	log10(10)	= 1
	1	1	log10(1)	= 0
	0.1	1 ÷ 10	log10(0.1)	= −1
	0.01	1 ÷ 10 ÷ 10	log10(0.01)	= −2
	0.001	1 ÷ 10 ÷ 10 ÷ 10	log10(0.001)	= −3
	.. etc..

Looking at that table, see how positive, zero or negative logarithms are really part of the same (fairly simple) pattern

( https://www.mathsisfun.com/algebra/logarithms.html )